0刖g當大型起重機作變幅運動時,吊臂作大范圍剛性轉動并伴隨小變形彈性運動,屬于剛柔耦合的多體動力學問題。但在以往的中,在求解起重機吊臂振動的固有頻率時,大都基于結構動力學理論,對吊臂的剛柔耦合運動考慮較少。當起重機吊臂長度較小如20m左右時,采用結構動力學方法可以對吊臂振動的固有頻率作近似計算,但如果吊臂較長,當起重機作變幅運動時,通過該方法得到的固有頻率就不十分準確,而柔性多體系統動力學正是解決與構件作剛柔耦合運相關的理論。在充分考慮起重機吊臂剛柔耦合運動特征的基礎上,依據柔性多體系統動力學理論,采用拉格朗日方程對起重機作變幅運動時吊臂在標稱運動附近作微振動的固有頻率進行了研究,計算結果較為精確。用這種方法得到的吊臂振動的固有頻率低于用傳統的結構動力學方法得到的結果,具有實際意義。
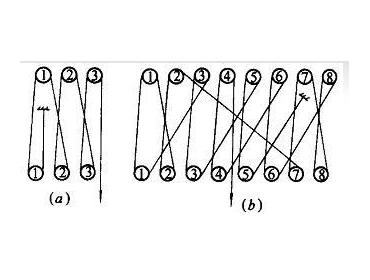
1采用拉格朗日方程建立機構動力學方程1.1假設變幅機構簡圖如所示。在變幅鋼絲繩2的牽引下完成變幅運動。在對吊臂1振動的固有頻率國家建設部攻關資助項目(03-2-039)。20050931收到初稿,20060407收到修改稿狀態矢童法的研究中,作如下假設。
變幅機構做平面運動。
吊鉤和滑輪組的質量集中在吊臂末端點C.吊重始終繞點C在吊重平面內單擺運動。
1.2建立坐標系,選取廣義坐標如所示建立坐標系,選取為慣性坐標系,坐標原點0選在卷筒中心;在吊臂上建立動坐標系Oifiyi,ci軸與未變形吊臂重合,坐標原點01選在吊臂與基座的鉸點,r為從慣性坐標系原點至吊臂上任一點p的矢徑,飫為0軸與Oc軸間的夾角令9為廣義坐標矢量qf――描述相對于動坐標系變形的廣義坐標矢量2.1吊臂在非線性慣性系下的振動方程由式(1)得非線性慣性系下,吊臂在標稱運動附近的振動方程為M――吊臂的廣義彈性質量矩陣M2ff――末端集中質量的廣義彈性質量矩陣0m吊臂質量m2端點集中質量吊臂變幅卷揚牽繩速度為0.71m.s'由此估算得吊臂繞定點轉動的*大角速度t.由于吊臂繞定點轉動的角速度小,此處忽略中項。
得反對稱矩陣2.2確定吊臂剛度矩陣吊臂的剛度矩陣由兩部分組成由于吊臂繞定點轉動的加速度遠低于不計剛柔耦合運動的吊臂振動的基頻,因此忽略動力剛度項的影響矩陣吊臂的彈性剛度矩陣可以通過相對于動坐標系的應變能求得=l-L.北京:冶金工業出版社,2000.師漢民,諶剛,吳雅。機械振動系統。武漢:華中理工大學出版社,1992.楊輝。剛一柔耦合動力學系統的建模理論與實驗研究。上海:上海交通大學,2002.曲秀全,陸念力。起重機吊臂和平衡臂的振動分析。起重運輸機械,2003,45(2):27-29.金則清。平衡共振問題探討。建筑機械,1994,15(8):29-31.equationStatevectorapproach:徐彥,女,1975年出生,博士研究生。主要從柔性多體系統動力學方面的研究。
 手機版|
手機版|

 關注公眾號|
關注公眾號|


 下載手機APP
下載手機APP